ANHANG

Algorithmen und Parameter für qualifizierte elektronische Signaturen

Anlage1

1. Definitionen

1. Signatursuite: Eine Signatursuite besteht aus folgenden Komponenten:

1. – einem Signaturalgorithmus mit Parametern,
2. – einem Algorithmus zur Schlüsselerzeugung,
3. – einem Padding-Verfahren und
4. – einer kryptographischen Hashfunktion.

2. Bitlänge: Die Bitlänge einer natürlichen Zahl p ist r, wenn 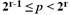gilt.

3. Kryptographische Hashfunktion: Der Algorithmus „Hash-Funktion“ ist eine nicht umkehrbare Funktion, die eine umfangreiche Datenmenge (in der Regel einen Text) auf eine im Allgemeinen wesentlich kleinere Zielmenge fester Länge (Hash-Wert) abbildet.

2. Abkürzungen

​

3. Zulässige Signatursuiten

Algorithmen und Parameter für qualifizierte elektronische Signaturen dürfen nur in vordefinierten Kombinationen verwendet werden, die als Signatursuiten bezeichnet werden.

Falls eine Komponente der Suite ungültig ist, ist auch die gesamte Suite ungültig. Falls eine Komponente der Suite aktualisiert worden ist, ist auch die gesamte Suite zu aktualisieren.

Tabelle 1a – Liste der zulässigen Signatursuiten:

​

Einige der in diesem Anhang gegebenen Algorithmen sind über Objektidentifikatoren registriert. Diese werden als Information in Tabelle 1b wiedergegeben.

Tabelle 1b – Objektidentifikatoren (OID)

​

4. Zulässige kryptographische Hashverfahren

Für qualifizierte elektronische Signaturen dürfen nur kollisionsresistente Hashfunktionen eingesetzt werden. Diese Voraussetzung ist erfüllt, wenn es rechnerisch nicht realisierbar ist, zwei Dokumente zu finden, die denselben Hashwert liefern.

Tabelle 2 – Liste der derzeit zulässigen Hashfunktionen

​

5. Zulässige Padding-Verfahren

Tabelle 3 – Liste der zulässigen Padding-Verfahren

​

6. Zulässige Signaturalgorithmen

Tabelle 4 – Liste der zulässigen Signaturalgorithmen

​

Tabelle 5 – Liste der zulässigen Schlüsselerzeugungsalgorithmen für die in Tabelle 4 aufgelisteten Signaturalgorithmen

​

7. Erläuterungen zu einzelnen Parametern der zulässigen Signaturalgorithmen

7.1 RSA

Die Sicherheit des RSA-Algorithmus beruht auf der Schwierigkeit, große ganze Zahlen zu faktorisieren. Um die Signaturerstellungsdaten und Signaturprüfdaten zu erzeugen, sind zufällig und unabhängig zwei Primzahlen p und q zu erzeugen, wobei die Bitlänge des Moduls n = pq mindestens MinModLen betragen muss; seine Länge wird auch als ModLen bezeichnet; Jede Primzahl muss effektiv von EntropyBits Bits tatsächlichem Zufall oder einem Ausgangswert der Länge SeedLen beeinflusst sein. p und q sollten etwa dieselbe Länge aufweisen, zB soll ein Bereich wie 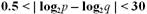festgelegt werden.

7.2 DSA

Die Sicherheit des DSA-Algorithmus beruht auf der Schwierigkeit, den diskreten Logarithmus in der multiplikativen Gruppe eines Primkörpers F_p zu berechnen.

Die Signaturerstellungsdaten bestehen aus

1. – den öffentlichen Parametern p, q und g,
2. – einer zufällig oder pseudozufällig erzeugten ganzen Zahl x, 0 xq, die signatorspezifisch ist, und
3. – einer zufällig oder pseudozufällig erzeugten ganzen Zahl k, 0 kq, die für jede Signatur neu zu erzeugen ist.

   Die öffentlichen Parameter p, q und g dürfen für eine Gruppe von Benutzern gleich sein. Der prime Modul p muss mindestens pMinLen Bits lang sein. q, das ein Primfaktor von (p-1) ist, muss mindestens qMinLen Bits lang sein.

Die Signaturprüfdaten bestehen aus p, q, g und einer ganzen Zahl y, die als y = g^x mod p berechnet wird.

7.2.1 DSA-Varianten mit elliptischen Kurven basierend auf einer Gruppe E(F_p)

Die Sicherheit des Algorithmus ecdsa-Fp beruht auf der Schwierigkeit, den diskreten Logarithmus über elliptischen Kurven zu berechnen.

Die öffentlichen Parameter sind wie folgt:

1. – p eine große Primzahl,

-qeine große Primzahl mit einer Länge von mindestens qMinLen Bits, ;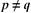

1. – E eine elliptische Kurve über dem endlichen Körper F_p, deren Ordnung durch q teilbar ist, und
2. – P ein fixer Punkt auf E mit der Ordnung q.

Die Klassenzahl der maximalen Ordnung des Endomorphismenrings von E muss mindestens MinClass betragen. Der Wert r₀:=min(r: q teilt p^r-1) muss größer als r0Min sein.

Die Signaturerstellungsdaten bestehen aus

1. – den öffentlichen Parametern E, q und P;
2. – einer statistisch einzigartigen und nicht voraussagbaren ganzen Zahl x, 0 xq, die signatorspezifisch ist und
3. – einer statistisch einzigartigen und nicht voraussagbaren ganzen Zahl k, 0 kq, die für jede Signatur neu zu erzeugen ist.

Die Signaturprüfdaten bestehen aus E, q, P und einem Punkt Q auf E, der als Q = xP berechnet wird. Die elliptische Kurve über F_p muss so gewählt werden, dass ihre Ordnung durch eine Primzahl q der Länge 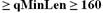teilbar ist.

7.2.2 DSA-Varianten mit elliptischen Kurven basierend auf einer Gruppe E(F2m)

Die Sicherheit des Algorithmus ecdsa-F2m beruht auf der Schwierigkeit, den diskreten Logarithmus über elliptischen Kurven zu berechnen.

Die öffentlichen Parameter sind wie folgt:

1. – m eine Primzahl,
2. – q eine große Primzahl mit einer Länge von mindestens qMinLen Bits,
3. – E eine elliptische Kurve über dem endlichen Körper F2m, deren Ordnung durch q teilbar ist,
4. – es darf nicht möglich sein, E über F₂ zu definieren, und
5. – P ein fixer Punkt auf E mit der Ordnung q.

   Die Klassenzahl der maximalen Ordnung des Endomorphismenrings von E muss mindestens MinClass betragen. Der Wert r₀:=min(r: q teilt 2^mr -1) muss größer als r0Min sein.

Die Signaturerstellungsdaten bestehen aus

1. – den öffentlichen Parametern E, q und m;
2. – einer statistisch einzigartigen und nicht voraussagbaren ganzen Zahl x, 0 xq, die signatorspezifisch ist, und
3. – einer statistisch einzigartigen und nicht voraussagbaren ganzen Zahl k, 0 kq, die für jede Signatur neu zu erzeugen ist.

Die Signaturprüfdaten bestehen aus E, q, P und einem Punkt Q auf E, der als Q = xP berechnet wird. Die elliptische Kurve über F2m muss so gewählt werden, dass ihre Ordnung durch eine Primzahl q der Länge 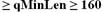teilbar ist.

7.2.3 EC-GDSA basierend auf einer Gruppe E(F_p)

Der ecgdsa-Fp Algorithmus ist eine Variante des ecdsa-Fp Algorithmus mit modifizierter Gleichung zur Signaturerstellung und modifiziertem Verfahren zur Signaturprüfung. Die Parameter sind dieselben wie für ecdsa-Fp.

7.2.4 EC-GDSA basierend auf einer Gruppe E(F2m)

Der Algorithmus ecgdsa-F2m ist eine Variante des Algorithmus ecdsa-F2m mit modifizierter Gleichung zur Signaturerstellung und modifiziertem Verfahren zur Signaturprüfung.

8. Erzeugung von Zufallszahlen

Tabelle 6 – Liste der zulässigen Verfahren zur Erzeugung von Zufallszahlen

​

8.1 Anforderungen an Zufallszahlengeneratoren trueran

Ein physikalischer Zufallszahlengenerator basiert auf einer physikalischen Rauschquelle (Primärrauschen) und einer kryptographischen oder mathematischen Nachbehandlung des Primärrauschens. Das Primärrauschen muss regelmäßig einer geeigneten statistischen Prüfung unterzogen werden. Der erwartete Aufwand des Erratens eines kryptographischen Schlüssels soll mindestens gleich groß sein, wie der Aufwand des Ratens eines Zufallswerts der Länge EntropyBits.

8.2 Anforderungen an Zufallszahlengeneratoren pseuran

Ein Pseudo-Zufallszahlengenerator muss mit einer echten Zufallszahl initialisiert werden. Der Anfangswert wird als „Seed“ bezeichnet und hat die Länge SeedLen. Die Ausgabe des Generators muss folgenden Anforderungen genügen:

1. – keine Information hinsichtlich der erzeugten Ausgabebits ist vorab bestimmbar;
2. – die Kenntnis einer Teilsequenz der Ausgabe erlaubt keinen Rückschluss auf ein verbleibendes Bit mit einer Wahrscheinlichkeit, die sich nicht-vernachlässigbar von Zufall unterscheidet;
3. – es gibt kein verwendbares Verfahren, um aus der Ausgabe des Generators eine zuvor generierte oder zukünftige Ausgabe, einen internen Status oder den Anfangswert („Seed“) zu erlangen.

Der erwartete Aufwand des Erlangens jedweden internen Status des Generators soll im Wesentlichen der Schwierigkeit des Erratens eines Zufallswerts der Länge SeedLen Bits sein.

Wenn der Generator mit mindestens SeedLen Bits initialisiert wurde, können bis zu n = 100 in Folge erzeugte Signaturerstellungsdaten gleichermaßen verwendet werden, als ob sie von einem Generator trueran erzeugt worden wären. Für die Massenproduktion (durch den ZDA) von k Schlüsseln, k > n ist es zulässig, dass zusätzlich zur initialen Entropieanforderung echter Zufall (von einem trueran Generator) langsam mit einer Rate von j = 8 Bits pro Ausgabewert beigegeben wird, andernfalls sollte der Generator komplett neu initialisiert werden.

Wenn Re-Initialisierung angewandt wird, muss die Sicherheit des Re-Initialisierungsprozesses zumindest so stark sein, wie die ursprüngliche Initialisierung und Prozeduren folgen, die der Erstellung von Root-Schlüsseln ähnlich sind. Die Re-Initialisierung von Smartcards ist nicht zulässig.

Keine Backups des Anfangswerts („Seed“) oder interner Stati von Pseudo-Zufallszahlengeneratoren sind zulässig.

Zusatzdokumente: image001, image002, image003, image004, image005, image006